3.Average Speed And Average Velocity

Difference Between Speed and Velocity

What is velocity?
Velocity is defined as the rate of change of displacement.

1. It is a vector quantity, both magnitude and direction are required to define it.
2. It's direction is same as that of displacement.
3. SI unit of velocity is m/s

What is speed?
Speed is defined as the rate of change in distance with respect to time.

1. It is a scalar quantity. Only magnitude is required to define the speed.
2. Speed and velocity both have same unit.

Velocity and speed are very important concepts in Kinematics. 
Now sometimes students ask questions like 

Is average speed = average velocity?

The answer is no, average speed is not equal to average velocity. This is because 
Average Speed = Total distance/Total time
Average Velocity = Total displacement/Total time 
Just like both displacement and distance are different, average speed and average velocity are also different for ex. Motion around a circular track.

3. Average velocity

• Consider a particle undergoing motion along a straight line i.e. particle is moving along X-axis.
• Here in this case X co-ordinate describing motion of the particle from origin O varies with time or we can say that X co-ordinate depends on time.
• If at time t=t₁ particle is at point P , at a distance x₁ from origin and at time t=t₂ it is at point Q at a distance x₂ from the origin then displacement during this time is a vector from point P to Q and is
  Δx=x2−x1               (1)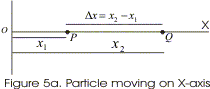 
  
  
  
   
  
• The average velocity of the particle is defined as the ratio of the displacement Δx of the particle in the time interval Δt=t₂-t₁. If v_avg represents average velocity then, 
  
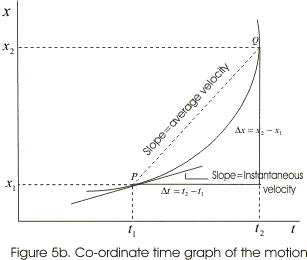
• Figure (5b) represents the co-ordinate time graph of the motion of the particle i.e., it shows how the value of x-coordinate of moving particle changes with the passage of time.
• In figure (5b) average velocity of the particle is represented by the slope of chord PQ which is equal to the ratio of the displacement Δx occurring in the particular time interval Δt.
• Like displacement average velocity v_avg also has magnitude as well as direction i.e.,average velocity is a vector quantity.
• Average velocity of the particle can be positive as well as negative and its positive and negative value depends on the sign of displacement.
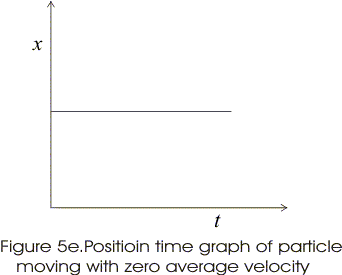
• If displacement of particle is zero its average velocity is also zero.
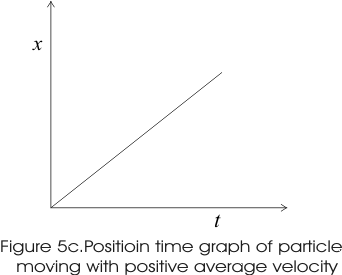
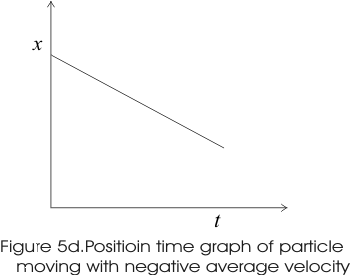
• Graphs below shows the x-t graphs of particle moving with positive, negative average velocity and the particle at rest.
  
  
  
  
  
  
  
  
  
  

average velocity definition

Average velocity is defined as the ratio of total displacement to total time. It is the average values of the velocities we know.

average velocity formula

This is extra section where we talk about average velocity formula. From average velocity definition we know that it is the ratio between total displacement and total time but this vav i.e., average velocity formula can have different form according to different problems. So before solving problems that asks you to find average velocity please check under which case your problem falls.

1. Case 1:-
   If X is total displacement of the body and t is the total time taken by the body to complete the displacement.The average velocity Vav is given by 
   
   vav=Total distance traveledtotal time taken=XT
2. Case 2:-
   If we know that body have initial displacement position x0 at time t0 undergoes a motion and attains final displacement xf at time tf then, the average velocity is given as
   
   vav=xf−x0tf−t0=Δ xΔ t
3. Case 3:-
   If we have a knowledge that x1,x2,.....xn are the distance covered by the body for time t1,t2,.....tn. The average velocity is 
   
   x1+x2+.......+xnt1+t2+.......+tn
4. Case 3:-
   If a velocity is changing as a result of a constant acceleration, the average velocity can be found by adding the initial and final velocities, and dividing by 2. Here it is important to note that this formula applies only for constant acceleration case. 
   Consider a body moving with uniform acceleration along a straight path. At some instant of time, initially its velocity is U m/s and at the end of t seconds let its final velocity be V m/s. Hence the average velocity is given as 
   
   vav=v+u2
   How to derive this average velocity formula
   Average velocity is displacement divided by time. Let us start with the formula for displacement and divide it by t.
   
   s=ut+12at2averagevelocity=ut+12at2t=u+12at=2u+at2=u+(u+at)2
   
   now, v=u+at 
   
   averagevelocity=u+v2

Average Speed

• From graph 5c it is clear that for positive average velocity slope of line slants upwards right or we can say that it has positive slope.
• For negative average velocity slope line slants upwards down to the right i.e. it has negative slope.
• For particles at rest slope is zero.
• So far we have learned that Average speed is defined as total distance traveled divided by time taken.
• Displacement of the object is different from the actual distance traveled by the particle.
• For actual distance traveled by the particle its average speed is defined as the total distance traveled by the particle in the time interval during which the motion takes place.
• Mathematically, 
  
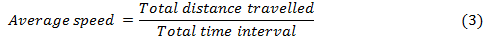
• Since distance traveled by an particle does not involve direction so speed of the particle depending on distance traveled does not involve direction and hence is a scalar quantity and is always positive.
• Magnitude of average speed may differ from average velocity because motion in case of average speed involve distance which may be greater than magnitude of displacement.
  
  Let us consider an example 
  
  here a man starts traveling from origin till point Q and return to point P then in this case displacement of man is
  Displacement from O to Q is OQ=80m
  Displacement from Q to P is =20m-80m=-60m
  total displacement of particle in moving from O to Q and then moving Q to P is = 80m + (-60m) = 20 m
  Now total distance traveled by man is OQ+OP=80m+60m=140m
  Hence during same course of motion distance traveled is greater then displacement.
• From this we can say that average speed depending on distance is in general greater than magnitude of velocity.

Let us now consider some of the solved examples for the concepts Average speed and Average velocity. Questions are important for understanding the concept. Try to understand these solved examples and then try to solve few questions on your own. 

Examples based on Average Speed

Question 1 A car travels first half distance between two places with a speed of 40 Km/hr and the rest half with a speed of 60 Km/hr. Find the average speed of the car.
Solution Let x be the total distance traveled by the car.
Time taken to travel first half distance t1=x/240=x80hr
Time taken to travel rest half distance t2=x/260=x120hr
Therefore Average speed = (Total distance)/(Total time) = x(x/80)+(x/120)=48Km/hr

Question 2 A point traveling along a straight line traverse one third the distance with a velocity v0. The remaining part of the distance was covered with velocity v1for half the time and with velocity v2 for the other half of the time. Find the mean velocity of the point averaged over the whole time of motion.
Solution Let s be the total distance. Let s3 be the distance covered in time t1 while the remaining distance 2s3 in time t2 second
s3=v0t1
t1=s3v0             (1)
and,
2s3=v1(t22)+v2(t22)
or, 
t2=4s3(v1+v2)            (2)
Average Velocity =st2+t1
or, Average Velocity =s(s3v0)+(4s3(v1+v2))=3v0(v1+v2)v1+v2+4v0 

Examples based on Average Velocity

Question 1 Usually "average speed" means the ratio of total distance covered to total the total time elapsed. However sometimes the phrase "average speed" can mean magnitude of average velocity. Are the two same?
Solution No, usually they have different meanings, as according to their definitions
Average speed is defined as total distance traveled divided by time taken and Average velocity is defined as change of displacement divided by the time taken. Now since distance traveled by any particle is either grater then the displacement or it is equal to the displacement , the velocity would be given as
vav≥|v⃗ av|
that is usually average speed is greater than the magnitude of average velocity.
For example if a body returns to its starting point after some motion, then as distance travel would be finite while displacement would be zero. So in this case average speed would be greater then zero but magnitude of average velocity would be equal to zero.
However in case of motion along the straight line without change in direction, magnitude of displacement would be equal to distance and two definitions would mean the same.
Question 2 A student argues that the mean velocity during an interval of time can also be expressed as v⃗ =v⃗ f+v⃗ i2 and this should always be equal to v⃗ =r⃗ f−r⃗ it2−t1 . is he right?
Solution: No, he is not right. The correct definition of average velocity is the later one.The first one can be used only when there is uniform acceleration.