6.Motion with constant acceleration

6.Kinematic equations for uniformly accelerated Motion

• Motion with constant acceleration or uniformly accelerated motion is that in which velocity changes at the same rate throughout motion.
• When the acceleration of the moving object is constant its average acceleration and instantaneous acceleration are equal. Thus from eq. 5 we have 
  
• Let v₀ be the velocity at initial time t=0 and v be the velocity of object at some other instant of time say at t₂=t then above eq. 7 becomes 
  a=v−v0t−0
  or , v=v₀+at                         (8)
• Graphically this relation is represented in figure 8 given below.
  
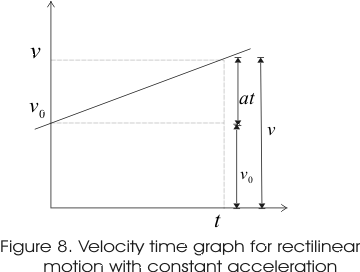
• Thus from the graph it can be seen clearly that velocity v at time t is equal to the velocity v₀ at time t=0 plus the change in velocity (at).
• In the same way average velocity can be written as 
  vavg=x−x0t−0
  where x₀ is the position of object at time t=0 and v_avg is the average velocity between time t=0 to time t.The above equation then gives
  x=x₀+v_avgt                    (9)
  
  Now we know that area under v-t curve represent the displacement
  So,
  x−x0=12(v−v0)t+v0t as ( Area of Triangle + Area of Rectangle)
  x−x0=v+v02t
  From equation 9 and the above equation we cay say that
  
  
  
  Now from eq. 8 we find
  v_avg = v₀ + ½(at)                    (11)
  putting this in eq. 9 we find 
  x = x₀ + v₀t + ½(at²) 
  or,
  x - x₀ = v₀t + ½(at²)                (12)
  this is the position time relation for object having uniformly accelerated motion.
• From eq. 12 it is clear that an object at any time t has quadratic dependence on time, when it moves with constant acceleration along a straight line and x-t graph for such motion will be parabolic in natures shown below.
  
  
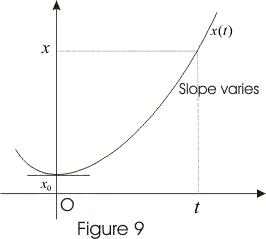
• Equation 8 and 12 are basic equations for constant acceleration and these two equations can be combined to get yet another relation for x , v and a eliminating t so, from 8 
  
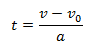
  putting this value of t in equation 12 and solving it we finally get,
  v² = (v₀)² + 2a ( x - x₀ )                     (13)
• Thus from equation 13 we see that it is velocity displacement relation between velocities of object moving with constant acceleration at time t and t=0 and their corresponding positions at these intervals of time.
• This relation 13 is helpful when we do not know time t.
  
  The above three equations are called the Kinematics equations
  v= v₀ + at
  x - x₀ = v₀t + ½(at²)
  v² = (v₀)² + 2a ( x - x₀ )
  
  If x₀ =0,then
  v= v₀ + at
  x= v₀t + ½(at²)
  v² = (v₀)² + 2a ( x) 
• Likewise we can also eliminate the acceleration between equation 8 and 12. Thus from equation 8
  
  
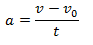
  putting this value of a in equation 12 and solving it we finally get,
  ( x - x₀ ) = ½ ( v₀ + v ) t               (14)
• Same way we can also eliminate v₀ using equation 8 and 12. Now from equation 8
  v₀ = v - atputting this value of v₀ in equation 12 and solving it we finally get,
  ( x - x₀ ) = vt - ½ ( at² )                (15)
  thus equation 15 does not involve initial velocity v₀
• Thus these basic equations 8 and 12 , and derived equations 13, 14, and 15 can be used to solve constant acceleration problems.

Obtaining Kinetmatics equations using Calculus Method
By defination,
a=dvdt
dv=adt
Integrating Both sides
∫dv=∫adt
∫dv=a∫dt ( as a is constant)
v-v₀ = at
v = v₀ + at

Now,
v=dxdt
dx= vdt
Integrating Both the sides
∫dx=∫vdt
or
∫dx=∫(v0+at)dt
x - x₀ = v₀t + ½(at²)

Now, a=dvdt=dvdxdxdt=vdvdx
or vdv=adx
Integrating Both sides
∫vdv=∫adx
v2−v202=a(x−x0)
v² = (v₀)² + 2a ( x - x₀ )
So we have easily derived all the Kinematics equations
The best advantages with calculus method is that we can use for non-uniform acceleration motion also

How to Solve Kinematics equations problem

1. Read the question carefully. 
2. Choose the origin of the coordinates and the axes wherever you would like to make calculation easiar
3. Choose one direction as positive . Usually we choose right of the x-axis as positive. The velocity and acceleration in the direction of positive axis will be positive and opposite direction will be negative
4. Find out the known and unknown. Consider quantities both at the start and end of the time interval.Also it would be good to translate some stated terms in physical quantities such as starting from rest means v₀=0
5. Check out which kinematics equation may be useful in this situation and solve accordingly to get the result.Sometime multiple equation may be required to get the solution
6. Check for answer If it is reasonable
7. Be careful about the units used. It should be same

Question
A boy throws a ball upwards with an initial speed of 20.0 m/s
(a) What is the direction of acceleration during the upward motion of the ball ?
(b) What are the velocity and acceleration of the ball at the highest point of its motion ?
(c) Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward, and downward motion.
(d) To what height does the ball rise and after how long does the ball return to the player's hands ? (Take g = 10 m/s² and neglect air resistance).

Solution
(a) Irrespective of the direction of the motion of the ball, acceleration (which is actually acceleration due to gravity) always acts in the downward direction towards the centre of the Earth.
(b) At maximum height, velocity of the ball becomes zero. Acceleration due to gravity at a given place is constant and acts on the ball at all points (including the highest point) with a constant value i.e., 10 m/s²
(c) During upward motion, the sign of position is positive, sign of velocity is negative, and sign of acceleration is positive. During downward motion, the signs of position, velocity, and acceleration are all positive.
(d) For Upward Motion
Initial velocity of the ball, u = - 20 m/s ( As upward direction and opposite direction to the positive we have choosen)
Final velocity of the ball, v = 0 (At maximum height, the velocity of the ball becomes zero)
Acceleration, a = +g = 9.8 m/s² ( As downward direction and same direction to the positive we have choosen)
From third equation of motion, height (s) can be calculated as:
v² = (v₀)² + 2a ( x - x₀ )

Now x=0
0²= (-20)² +2(10)( 0-x)
x= 20 m

Let t be the time taken to reach the highest point
From First equation of motion
v=u + at
0=-20+ 10t
t= 2sec

As Time of ascent = Time of descent
Hence, the total time taken by the ball to return to the boy hands = 2 + 2 = 4 s.