7. Uniform circular motion

7. Uniform circular motion

• When an object moves in a circular path at a constant speed then motion of the object is called uniform circular motion.
• In our every day life ,we came across many examples of circular motion for example cars going round the circular track and many more .Also earth and other planets revolve around the sun in a roughly circular orbits
• Here in this section we will mainly consider the circular motion with constant speed
• if the speed of motion is constant for a particle moving in a circular motion still the particles accelerates becuase of costantly changing direction of the velocity.
• Here in circular motion ,we use angular velocity in place of velocity we used while studying linear motion

(A) Centripetal Acceleration 
Now when a particle moves along a circular path it must have components of acceleration perpendicular to the path when its speed is constant. Such type of circular motion is called Uniform circular motion . For this article consider  the particle moves in a circular path with constant speed. Here in this article we will discuss how to drive relation between the normal component of acceleration , the particle's speed and radius of the path.
To understand this consider the figure given below

This figure represent a particle that is moving in circular path of radius R and have its center at O. Here vectors v1 and v2 represents the velocities at points P and Q respectively.  Figure given below shows the vector change in velocity that is Δv as the particle moves from P to Qin time Δt.
 

The triangle OPQ in first figure and triangle opq in second figure are similar since both are isosceles triangles and the angles labeled Δθ in both the triangles are same. Hence we have
Δvv1=ΔsR
or
Δv=v1RΔs
Let |a⊥| be the magnitude of average normal acceleration during time Δt and is equal to ΔvΔt. So from above equation we get
|a⊥|=ΔvΔt=v1RΔsΔt
So the instantaneous acceleration a⊥ at point P is the limiting value of this expression as we take point Q to point P and Δt→0
So,
a⊥=limΔt→0(v1RΔsΔt)=v1RlimΔt→0(ΔsΔt)
But the limiting value of ΔsΔt is the speed v1 of the particle at point P . Since P can be any point in the path , we can conveniently drop the subscript from v1 and let v represents the speed of the particle at any point in the circular path. So
a⊥=v2R
So , from the above equation we can say that

The magnitude of the instantaneous normal acceleration is equal to the square of the speed divided by the radius. Its direction is perpendicular to v and acts along inward direction along the radius of the circular path towards the center  of the circle.

Because of this it is called central or centripetal acceleration. The term centripetal means seeking the center.
So far we have discussed circular motion physics with particle moving with constant speed. If the speed varies then above equation for normal acceleration or centripetal acceleration still holds but in case of varying speed you also have a tangential component of acceleration a∥, equal of the rate of change of speed. So,
a∥=limΔt→0(Δv∥Δt)
So if the speed is constant then there is no tangential acceleration. In this case acceleration is purely normal . This normal acceleration is result of the continuous change in direction of the velocity.

(B) Angular velocity

• Consider an object moving in a circle with uniform velocity v as shown below in the figure
  
  
   
  
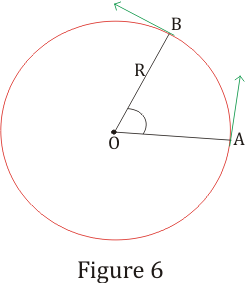
  The velocity v at any point of the motion is tangential to the circle at that point.Let the particle moves from point A to point Balong the circumference of the circle .The distance along the circumference from A to B is
  s=Rθ                                          (23)
  Where R is the radius of the circle and θ is the angle moved in radian's
• Magnitude of velocity is
  v=ds/dt=Rdθ/dt                                          (24)
  Since radius of the circle remains constant quantity,
  ω=dθ/dt                                          (25)
  is called the angular velocity defined as the rate of change of angle swept by radius with time.
• Angular velolcity is expressed in radians per second (rads^-1)
• From equation 24 and 25,we find the following
  v=ωR                                          (26)
• Thus for a particle moving ain circular motion ,velocity is directly proportional to radius for a given angular velocity
• For uniform circular motion i.e, for motion with constant angular velocity the motion would be periodic which means particle passes through each point of circle at equal intervals of time
• Time period of motion is given by
  T=2π/ω                                          (27)
  Since 2π radians is the angle θ in one revolution
• If angular velocity ω is constant then integrating equation (25) with in limits θ₀ to θ,we find
  
   
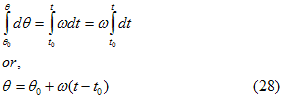
  where θ₀ is the angular position at time t₀ and θ is the angular position at time t .The above equation is similar to rectilinear motion result x-x₀=v(t-t₀)

(B) Angular acceleration

• Angular acceleration is defined as the rate of change of angular velocity moving in circular motion with time.
  Thus
  α=dω/dt=d²θ/dt²                                          (29)
  Unit of angular acceleration is rads^-2
• For motion with constant angular acceleration
  
   
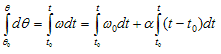
  or 
  ω=ω₀+α(t-t₀)                                          (30)
  where ω₀ is the angular velocity at time t₀
  Again since
  ω=dθ/dt 
  or dθ=ωdt then from equation 30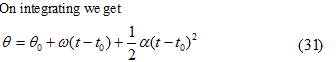 
   
  If in the begining t₀=0 and θ₀=0 the angular position at any time t is given by
  θ=ωt+(1/2)αt²
  This result is of the form similar to what we find in case of uniformly accelerated motion while studying rectilinear motion
  
  

Question An particle is present on the tip of the fan blade .15 m of radius rotating at 20 rev/sec
(a) What is the angular speed, and the linear speed of the motion of the particle?
(b) Is the acceleration vector a constant vector ? What is its magnitude ? What is its direction?
Solution
This is an classic example of uniform circular motion.
a) Given
R = .15 m.
Frequency = 20 rev/sec
The angular speed ω is given by
ω = 2π(freq) = 2π (20) = 40π rad/s
The linear speed v is :
v =ω R = (40π) (.15) = 18.84 m/s
The direction of velocity v is along the tangent of the circle at every point
b) We know in circular motion,The acceleration is directed towards the centre of the circle. Since this direction changes continuously, acceleration here is not a constant vector.
However, the magnitude of acceleration is constant:
a = ω² R = (40π)² (.15 m)
= 2368.8 m/s²